Tā ir nožēlojama realitāte, ka nekad nav pietiekami daudz laika, lai aptvertu visus interesantos zinātniskos stāstus, ar kuriem mēs katru mēnesi sastopamies. Iepriekš mēs esam piedāvājuši gada beigu apkopojumus par foršiem zinātnes stāstiem, kurus (gandrīz) palaidām garām. Šogad mēs eksperimentējam ar ikmēneša kolekciju. Oktobra sarakstā ir iekļautas mikrostrukturālās atšķirības starp parastajiem un bezglutēnu spageti, pārsteidzošu čūsku notveršana darbībā, Marsa gravu veidošanās noslēpums un — visiem vārdu spēļu entuziastiem — intriģējošs skaitļošanas pierādījums par augstāko iespējamo punktu skaitu Boggle dēļa.
Visaugstākais punktu skaits Boggle dēlis
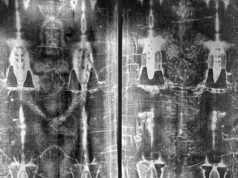
Dažreiz mēs saņemam noderīgus stāstu padomus no lasītājiem par neparasti interesantiem pētniecības projektiem. Dažreiz šie projekti ietver tādas klasiskas spēles kā Apjukumskurā spēlētāji noteiktā laika limitā atrod pēc iespējas vairāk vārdu no 4 × 4 režģa, kurā ir 16 burtu kubiskie kauliņi. Programmatūras inženieris Dens Vanderkams mūs brīdināja par a priekšdruka viņš ievietoja fizikas arXiv, detalizēti aprakstot savus meklējumus, lai atrastu Boggle dēļa konfigurāciju, kas dod augstāko iespējamo rezultātu. Tas ir attēlots iepriekš ar kopējo punktu skaitu 3625 punktos, saskaņā ar Vanderkama pirmo skaitļošanas pierādījumu. Ir vairāk nekā 1000 iespējamo vārdu, un “pārapmetums” ir visilgākais.
Vanderkam ir dokumentēja savus meklējumus un tā izšķirtspēju (tostarp viņa izmantoto kodu) plaši viņa emuārā, atzīst Financial Times ka: “Cik es varu pateikt, es esmu vienīgais cilvēks, kuru šī problēma patiešām interesē.” Tā nav gluži taisnība: 1982. gadā tika mēģināts atrast optimālu dēli, kas ienesa 2195 punktus. Vanderkama dēlis bija zināms kā, iespējams, ar visaugstāko punktu skaitu, taču to bija ļoti grūti pierādīt, izmantojot standarta heiristiskās meklēšanas metodes. Vanderkam risinājums ietvēra dēļu konfigurāciju ar līdzīgiem modeļiem grupēšanu klasēs un pēc tam augšējo robežu atrašanu, lai atmestu skaidrus zaudētājus, nevis mēģinātu saskaitīt katras plates rezultātus atsevišķi, ti, vecās skolas “zaru un saišu” paņēmienu.